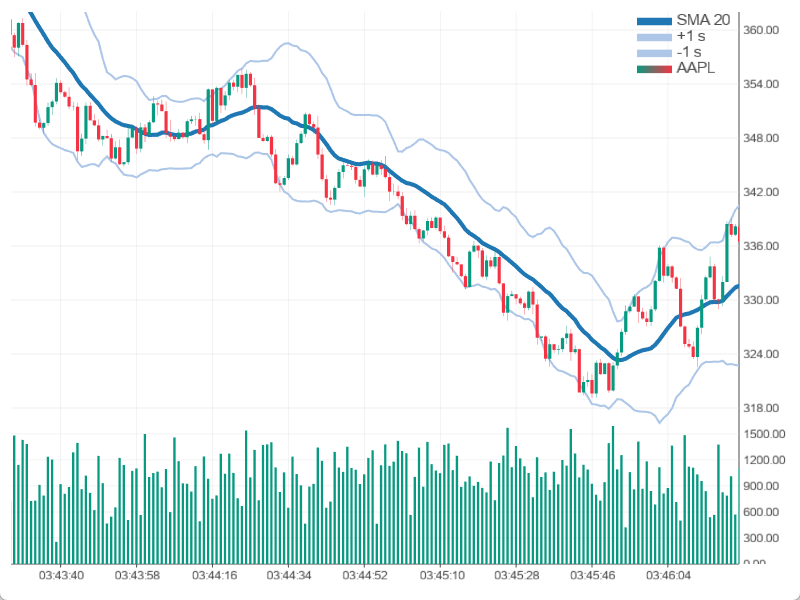
Plot with Volume and Bollinger Bands

This example shows how rallyplot can be used to plot real indicators over a candlestick plot. Here we compute a rolling mean and standard deviation (20 samples).

Python

from rallyplot import Plotter
from rallyplot import get_toy_candlestick_data
import numpy as np

open_high_low_close_df, volume, dates = get_toy_candlestick_data(N=100_000)

mean = open_high_low_close_df["close"].rolling(window=20).mean()
std = open_high_low_close_df["close"].rolling(window=20).std()
std_upper = mean + 2 * std
std_lower = mean - 2 * std

plotter = Plotter(anti_aliasing_samples=8)

plotter.line(
    mean,
    dates,
    color=(0.1216, 0.4667, 0.7059),
    width=1.5
)

for arr in [std_upper, std_lower]:

    plotter.line(
        arr,
        color=(0.6824, 0.7804, 0.9098),
        width=0.75
    )

# plot the candlestick last so it is on top
plotter.candlestick_from_df(open_high_low_close_df)

plotter.set_legend(
    ["SMA 20", "+1 s", "-1 s", "AAPL"]
)

plotter.add_linked_subplot(0.25)

plotter.bar(volume, min_value=0)

plotter.start()

C++

#include <Plotter.h>
#include <ToyData.h>
#include <vector>

struct BollingerOutput
{
    std::vector<float> rollingMean;
    std::vector<float> stdUpper;
    std::vector<float> stdLower;
};

BollingerOutput computeBollinger(const std::vector<float>& data)
/*
    A quick function to compute rolling mean and 2x std with
    pre-determined window size (20).
 */
{
    int n = data.size();
    std::vector<float> rollingMean(n);
    std::vector<float> stdUpper(n);
    std::vector<float> stdLower(n);

    int nTimesStd = 2;
    int W = 20;
    double mean = 0;
    double S1 = 0;
    for (int i = 0; i < W; i++)
    {
        mean += data[i];
        S1 += data[i]*data[i];

        rollingMean[i] = std::numeric_limits<float>::quiet_NaN();
        stdUpper[i] = std::numeric_limits<float>::quiet_NaN();
        stdLower[i] = std::numeric_limits<float>::quiet_NaN();
    }
    mean = mean / W;
    S1 = S1 / W;

    double var;
    for (int i = W; i < n; i++)
    {
        mean = mean - data[i - W] / W + data[i] / W;
        S1 = S1 - data[i - W]*data[i - W] / W + data[i]*data[i] / W;

        var = S1 - mean*mean;
        if (var < 0.0) var = 0.0;

        rollingMean[i] = mean;
        stdUpper[i] = mean + std::sqrt(var) * nTimesStd;
        stdLower[i] = mean - std::sqrt(var) * nTimesStd;
    }

    return BollingerOutput{
        rollingMean, stdUpper, stdLower
    };
}


int main(int argc, char* argv[])
{

    CandleData candleData = getToyCandlestickData(100000);

    BollingerOutput bollingerOutput = computeBollinger(candleData.close);

    PlotterArgs plotterArgs{};
    plotterArgs.antiAliasingSamples = 8;

    Plotter plotter = Plotter(plotterArgs);

    LineSettings lineSettings{};
    lineSettings.color = {0.1216, 0.4667, 0.7059};
    lineSettings.width = 1.5f;

    plotter.line(
        bollingerOutput.rollingMean,
        candleData.dates,
        lineSettings
    );

    lineSettings.color = {0.6824, 0.7804, 0.9098};
    lineSettings.width = 0.75f;

    plotter.line(bollingerOutput.stdLower, lineSettings);
    plotter.line(bollingerOutput.stdUpper, lineSettings);
    
    // plot the candlestick last so it is on top
    plotter.candlestick(
        candleData.open, candleData.high, candleData.low, candleData.close, candleData.dates
    );


    plotter.addLinkedSubplot(0.25);

    plotter.bar(candleData.volume);

    plotter.start();

}